m1-ENSL/CGDI
1
0
Fork 0
Code Issues Pull Requests Actions Packages Projects Releases Wiki Activity

Cleanup

Browse Source
This commit is contained in:
David Coeurjolly 2023-01-10 11:07:10 +01:00
parent 8aa50efbd0
commit 97cd9c7871
3 changed files with 0 additions and 443 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

151
notes_backup/1_SOT.md
View File

@ -1,151 +0,0 @@
[CGDI] Color Transfer via Discrete Optimal Transport using the *sliced* approach
==
> [name="David Coeurjolly"]
ENS [CGDI](https://perso.liris.cnrs.fr/vincent.nivoliers/cgdi/) Version
[TOC]
---
Color transfer is an image processing application where you want to retarget the color histogram of an input image according to the color histogram of a target one.
**Example:**
Input image | Target image | Color transfer output
-------|---------|----
![](https://raw.githubusercontent.com/dcoeurjo/transport-optimal-gdrigrv-11-2020/main/pexelA-0.png) | ![](https://raw.githubusercontent.com/dcoeurjo/transport-optimal-gdrigrv-11-2020/main/pexelB-0.png) | ![](https://raw.githubusercontent.com/dcoeurjo/transport-optimal-gdrigrv-11-2020/main/output.png)
The idea of this project is to detail a color transfer solution that considers
the [Optimal Transport](https://en.wikipedia.org/wiki/Transportation_theory_(mathematics)) as a way to *deform* histograms in the most *efficient way* (see below for details).
The objective of this TP is to implement a *sliced* approach to solve the color transfer problem via Optimal Transport.
# Warm-up 1: Downloading the code
The skeleton of the code is available on [this Github Project](https://github.com/dcoeurjo/transport-optimal-gdrigrv-11-2020). This code contains all you need to load and save color images (and to parse command line parameters for the `c++`code). You can download the archive from the Github interface (*"download zip"* menu), or *clone* the git repository. The project contains some `c++` and `python` codes.
:::warning
For python, we encourage you to use the notebooks shared by Vincent on the [CGDI homepage](https://perso.liris.cnrs.fr/vincent.nivoliers/cgdi/).
:::
To compile the C++ tools, you would need [cmake](http://cmake.org) (>=3.14) to generate the project. For instance on linux/macOS:
``` bash
git clone https://github.com/dcoeurjo/CGDI-Practicals
cd CGDI-Practicals/1-SlicedOptimalTransport
cd c++
mkdir build ; cd build
cmake .. -DCMAKE_BUILD_TYPE=Release
make
```
On Windows, use cmake to generate a Visual Studio project.
The practical work described below can be done either in `c++` or `python`.
In the next section, we briefly introduce Optimal Transport and Sliced Optimal Transport (you can skip this section if you have followed the lecture).
# Warm-up 2: Elementary Histogram Processing
Either in `c++` and `python`, implement several basic histogram processing tools you have already discussed in the lecture:
1. RGB -> Grayscale transform: Just convert a color image to a single channel grayscle one.
2. [Gamma correction](https://en.wikipedia.org/wiki/Gamma_correction) (each channel of the RGB images will be processed independently).
# Brief overview:  Optimal Transport and Sliced Optimal Transport
As mentioned above, the key tool will be Optimal Transport (OT for short) which can be sketched as follows: Given two probability (Radon) measures $\mu\in X$ and $\nu\in Y$, and a *cost function* $c(\cdot,\cdot): X\times Y \rightarrow \mathbb{R}^+$, an optimal transport plan $T: X\rightarrow Y$ minimizes
$${\displaystyle \inf \left\{\left.\int _{X}c(x,T(x))\,\mathrm {d} \mu (x)\;\right|\;T_{*}(\mu )=\nu \right\}.}$$
The cost of the optimal transport defines a metric between Radon measure. We can define the $p^{th}$ [Wasserstein metric](https://en.wikipedia.org/wiki/Wasserstein_metric), $\mathcal{W}_p(\mu,\nu)$ as
$$\displaystyle \mathcal{W}_{p}(\mu ,\nu ):={\left(\displaystyle \inf \left\{\left.\int _{X}c(x,T(x))^p\,\mathrm {d} \mu (x)\;\right|\;T_{*}(\mu )=\nu \right\}\right)^{1/p}}$$
An analogy with piles of sand is usually used to explain the definition: let us consider that $\mu$ is a pile of sand and $\nu$ a hole (with the same *volume* or *mass*), if we consider that the cost of moving an elementary volume of sand from on point to the other is proportional to the Euclidean distance ($l_2$ cost function), then the optimal transport plan gives you the most efficient way to move all the sand from $\mu$ to $\nu$. Again, the literature is huge and there are many alternative definitions, please refer to [Computational Optimal Transport](https://optimaltransport.github.io/book/) for a more complete introduction to the subject.
The link between OT and color transfer follows the observation that color histograms are discrete Radon measures. As we are looking for the *most efficient* transformation of the input image histogram to match with the target one, the color transfer problem can be reformulated as a discrete OT one [^b1][^b2][^b2b][^b3][^b4][^b5].
There are many numerical solutions to compute the OT (with continuous, discrete, semi-discrete measures, w/o regularization...). We focus here on the **sliced** formulation of the OT and associated 2-Wasserstein metric in dimension $d$:
$$ SW^2_2(\mu,\nu) := \int_{\mathbb{S}^d} \mathcal{W}_2^2( P_{\theta,\sharp}\mu,P_{\theta,\sharp}\nu) d\theta\,.$$
The sliced formulation consists in projecting the measures onto a 1D line ($P_{\theta,\sharp}: \mathbb{R}^d\rightarrow \mathbb{R}$), solving the 1D OT problem on the projections and average the results for all directions ($\mathbb{S}^d$ is the unit hypersphere in dimension $d$).
If the measures are discrete as the sums of Diracs centered at points $\{x_i\}$ and $\{y_i\}$ in $\mathbb{R}^d$ ($\mu := \frac{1}{n}\sum_{x_i} \delta_{x_i}$, $\nu := \frac{1}{n}\sum_{y_i} \delta_{y_i}$), then the 1D OT is obtained by sorting the projections and computing the difference between the first projected point of $\mu$ with the first projected point of $\nu$, the second with the second, etc...
$$ SW^2_2(\mu,\nu) = \int_{\mathbb{S}^d} \left(|\langle x_{\sigma_\theta(i)} - y_{\kappa_\theta(i)},\theta\rangle|^2 \right) d\theta\,,$$
($\sigma_\theta(i)$ a,d ${\kappa_\theta(i)}$ are permutations with increasing order).
Numerically, we sample the set of directions $\mathbb{S}^d$ and thus consider a finite number of *slices*.
# Sliced OT Color Transfer, the "TP"
Back to our histogram transfer problem, Diracs centers $\{x_i\}$ are points in RGB space (one Dirac per pixel of the input image), and $\{y_i\}$ are the colors of the target image. Matching the histogram can be seen a transportation of the point cloud $\mu$ to $\nu$ in $\mathbb{R^3}$ (the RGB color space).
The idea is to advect points of $\mu$ such that we minimize $SW(\mu,\nu)$. As described in the literature[^b1][^b2b][^b4], this amounts to project he points onto a random direction $\theta$, *align* the sorted projections and advect $\mu$ in the $\theta$ direction by $|\langle x_{\sigma_\theta(i)} - y_{\kappa_\theta(i)},\theta\rangle|$.
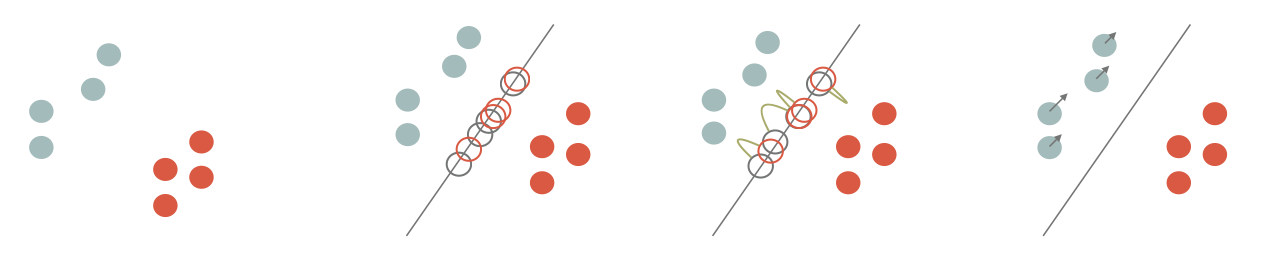
![](https://dcoeurjo.github.io/OTColorTransfer/images/sliced.png)
### The core
3. Get the `C++` / `python`. In Both cases, we provide elementary code to load/save RGB images. Please check how to access to RGB pixel values.
2. Create a function to draw a random direction
::: info
**Info**: to uniformly sample a direction in $\mathbb{R}^d$, a classical approach is to draw a $d$ dimensional random vector where each component follows a normal distribution (e.g. using C++ `std::normal_distribution`), with mean 0 and standard deviation equal to 1.0. Then normalize the vector and you have a uniform sampling of $\mathbb{S}^d$.
:::
3. From now on, the source (or target) image will be seen as a 3d point cloud in RGB space. Create a function to sort the projection of the samples of one image onto a random direction.
:::info
**Tip**: consider using a custom sort predicate in the C++ `std::sort` function.
:::
4. On this random direction $\theta$, sort both sample sets (source and target one) and advect the first sample, denoted $p_i$, of the source, along the $\theta$ direction, by an amount $d$ which correspond to the difference between projection of this first source sample, and the projection of the first target sample. In other words:
$$\vec{Op_i} = \vec{Op_i} + \langle x_{\sigma_\theta(0)} - y_{\kappa_\theta(0)},{\theta}\rangle ~{\theta}\,.$$
Do the same for the second ones, and the remaining samples.
:::info
**Tip**: Be careful when performing some computations on RGB `unsigned char` values. A good move would be to convert all data to `double` from the very beginning (and convert them back to `unsigned char` before exporting).
:::
5. Implement the main loop of the sliced approach: repeat the steps (draw a direction, sort the projections, compute the displacements, advect the source sample) until a maximum number of steps is reached.
6. To better set the maximum number of slices, output the sliced optimal transport energy with respect to the number of slices. You should also be able to *visualize* the convergence:
{%youtube FiVPXl3Io0w%}
### Advanced features
7. **Batches.** Instead of advecting $\mu$ for each $\theta$, we can accumulate advection vectors into a small batch and perform the transport step once the batch is full[^b4]. This corresponds to a stochastic gradient descent strategy in ML. Implement this "batch" approach. Compare this approach w.r.t to the legacy one (in terms of speed of convergence for instance).
8. **Regularization.** To obtain a smoother result or to be able to handle noise in the inputs, a classical approach consists in considering *regularized* optimal transport, or to regularize the optimal transport plan at the end of the computation. For color transfer, a simple way to mimic this approach consists in applying a non-linear smoothing filter to the transport plan[^b4]. A way to achieve this is to:
* once the sliced approach has converged, let's say we have a transformed source image $S^*$ of the image $S$ w.r.t. the target $T$;
* we express the transport plan as an *image* $(S^*-S)$;
* we can filter this image (using for instance a [bilateral filter](https://en.wikipedia.org/wiki/Bilateral_filter)) to obtain the final image : $\tilde{~S} = S + filter_\sigma(S^*-S)$.
:::info
**Tip**: In the `c++` project, we have included the [cimg](https://cimg.eu) header which contains an implementation of the bilateral filter. On `python`, the [OpenCV](https://opencv.org) package has been imported (which also contains an implementation of the bilateral filter).
:::
9. **Interpolation**: One can mimic the interpolation between two discrete measures in the sliced formulation by simply tweaking the advection step: instead of computing $\vec{Op_i} = \vec{Op_i} + \langle x_{\sigma_\theta(0)} - y_{\kappa_\theta(0)},{\theta}\rangle ~{\theta}$, just compute $\vec{Op_i} = \vec{Op_i} + \alpha\langle x_{\sigma_\theta(0)} - y_{\kappa_\theta(0)},{\theta}\rangle ~{\theta}$ for some $\alpha\in[0,1]$. You should be able to obtain something like that:
{%youtube Ti6kjJSdRnA%}
10. **Partial optimal transport**: as you may have noticed, the source and target images **must** have the same number of pixels. When the two discrete measures do not have the same number of Diracs, we are facing a *partial* optimal transport problem[^b6] (the overall all *sliced* approach remains the same, the 1D OT problem along the direcrtion is slightly more complicated). Without going to this *exact* partial solution, could you imagine and implement an approximate solution that *does the job* when the two images do not have the same size?
# References
[^b1]: Francois Pitié, Anil C. Kokaram, and Rozenn Dahyot. 2005. N-Dimensional Probablility Density Function Transfer and Its Application to Colour Transfer. In Proceedings of the Tenth IEEE International Conference on Computer Vision - Volume 2 (ICCV ’05). IEEE Computer Society, Washington, DC, USA, 1434–1439. https://doi.org/10.1109/ ICCV.2005.166
[^b2]: François Pitié, Anil C Kokaram, and Rozenn Dahyot. 2007. Automated colour grading using colour distribution transfer. Computer Vision and Image Understanding 107, 1-2 (2007), 123–137.
[^b2b]: Rabin Julien, Gabriel Peyré, Julie Delon, Bernot Marc, Wasserstein Barycenter and its Application to Texture Mixing. SSVM’11, 2011, Israel. pp.435-446. hal-00476064
[^b3]: Nicolas Bonneel, Julien Rabin, G. Peyré, and Hanspeter Pfister. 2015. Sliced and Radon Wasserstein Barycenters of Measures. J. of Mathematical Imaging and Vision 51, 1 (2015).
[^b4]: Julien Rabin, Julie Delon, and Yann Gousseau. 2010. Regularization of transportation maps for color and contrast transfer. In Image Processing (ICIP), 2010 17th IEEE International Conference on. IEEE, 1933–1936.
[^b5]: Nicolas Bonneel, Kalyan Sunkavalli, Sylvain Paris, and Hanspeter Pfister. 2013. Example- Based Video Color Grading. ACM Trans. Graph. (SIGGRAPH) 32, 4 (2013).
[^b6]: Nicolas Bonneel and David Coeurjolly. 2019. Sliced Partial Optimal Transport. ACM Trans. Graph. (SIGGRAPH) 38, 4 (2019).

140
notes_backup/2_rasterization.md
View File

@ -1,140 +0,0 @@
[CGDI] Rasterization, z-Buffer and Winding Numbers
===
> [name="David Coeurjolly"]
ENS [CGDI](https://perso.liris.cnrs.fr/vincent.nivoliers/cgdi/) Version
[TOC]
---
The objective of the practical is to play with basic 2D geometrical predicates illustrated using the [rasterization](https://en.wikipedia.org/wiki/Rasterisation) problem.
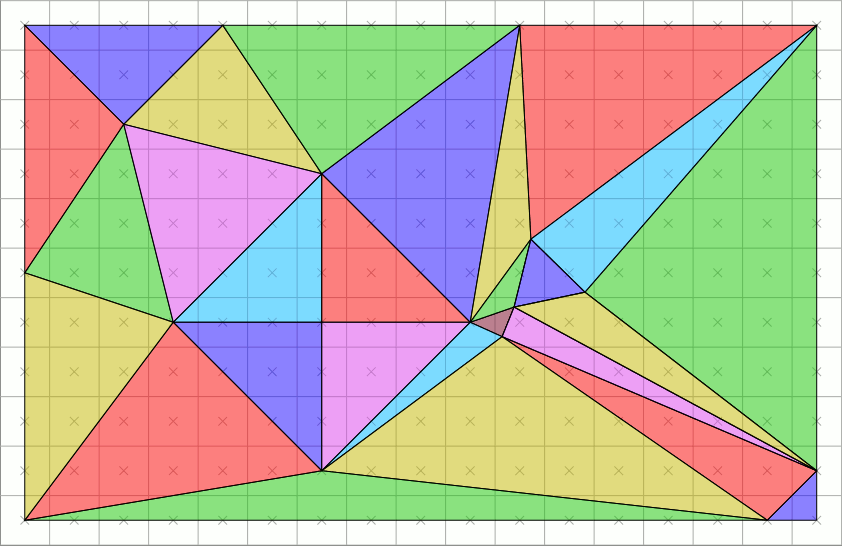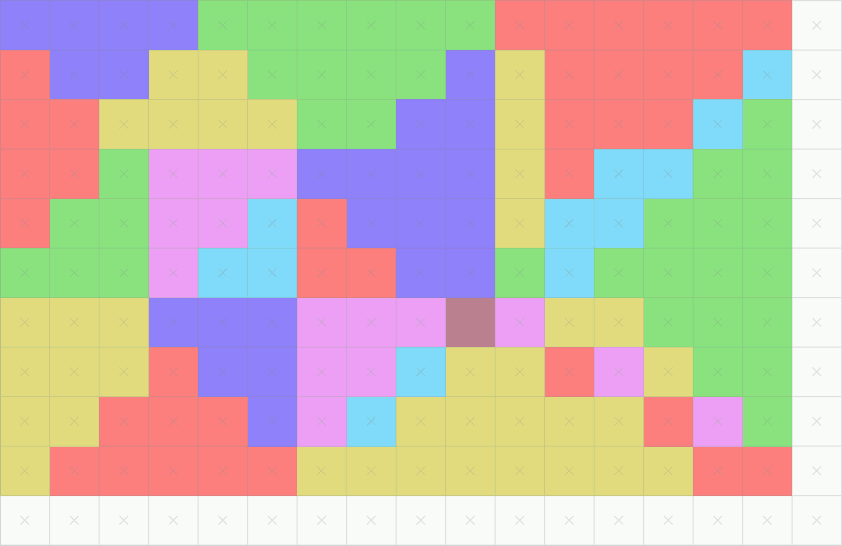![](https://upload.wikimedia.org/wikipedia/commons/b/b0/Top-left_triangle_rasterization_rule.gif)([wikipedia](https://commons.wikimedia.org/wiki/File:Top-left_triangle_rasterization_rule.gif))
The initial problem is quite simple: Given a triangle $\mathcal{T}$ in the plane (with vertices in $\mathbb{R}^3$), we want to construct the set of grid points $T$ such that $T:= D(\mathcal{T}):=\mathcal{T}\cap \mathbb{Z}^2$.
# Rasterization of triangles
:::danger
There is no special code for this practical. You would just need to be able to define and export an image. Please refer to the first practical for `python` and `c++` code snippets for that.
:::
## Playing with orientation predicate
From the lecture notes, given threep points $p,q,r\in\mathbb{R}^2$, we can design a simple determinant test to decide if $r$ lies on the *left*, on the *right*, or on the (oriented) straight line $(pq)$.
![](https://perso.liris.cnrs.fr/david.coeurjolly/teaching/ENS2019/slides/_images/signdet.png =400x200)
This can be done by considering an $Orientation(p,r,r)$ predicate defined as the sign of the determinant of $(\vec{pq}, \vec{pr})$ (aka the **signed** area of the parallelogram defined by $\vec{pq}$ and $\vec{pr}$).
1. Set up a rasterization project with to implement the following problem: Given an image $[0,0]\times[width,height]$, a triangle $\mathcal{T}$ in that domain, we would like to highlight the pixels **inside or on** $\mathcal{T}$.
2. From the orientation predicate, how can you implement a `isInside(p,q,r,pixel)->{true, false}` predicate? Implement such function for a single triangle T and use it to solve the initial rasterization problem.
:::info
**Hint:** Make sure to have edges of $\mathcal{T}$ properly oriented...
:::
3. For sure, `isInside(p,q,r,pixel)` should be in $O(1)$ and beside fancy sign of determinant computation tricks, there is very few thing you can do to optimize the process. However, to rasterize a complete triangle $\mathcal{T}$, can you imagine further optimization?
4. Now, we are considering a collection of triangles $\{\mathcal{T}_i\}_N$ (with a unique color per triangle). Obviously, we can loop on the function of the question 2, but what can you do to optimize the computations?
5. For two adjacent triangles $\mathcal{T}_1,\mathcal{T}_2$(ie. sharing an edge), do you have ${T}_1\cap {T}_2\neq\emptyset$ ? $D({\mathcal{T}_1\cup \mathcal{T}_2}) = T_1 \cup T_2$ ? Please experiment and comment.
6. Update a bit the `isInside(p,q,r,pixel)` function to also highlight pixel which lies exactly on an edge (e.g. use a different color for such points in the rasterization).
:::warning
Conservative vs. non-conservative raterization, and optimized code are important bottleneck issues in GPU designs. See for instance [nvidia](https://developer.nvidia.com/gpugems/gpugems2/part-v-image-oriented-computing/chapter-42-conservative-rasterization) notes.
:::
8. **Extra (Hurt Me Plenty.)** For an infinite straight-line $(pq)$ with $p,q\in\mathbb{R}^2$, what are the conditions for $p$ and $q$ to have $(pq)\cap\mathbb{Z}^2\neq \emptyset$?
9. **Extra (Ultra-Violence)** For $p\in\mathbb{Z}^2$, what are the solutions of $(Op)\cap\mathbb{Z}^2$.
10. **SuperExtra (Nightmare)** Given a 2D convex polygon with $N$ vertices, design a sub-linear "Point-in-Polygon" test. If the polygon is not convex (but *simple*), design a linear in time algorithm for the "Point-in-Polygon" test.
## Barycentric coordinates
An alternative way to rasterize a triangle is to consider an area-based technique which is deeply linked to [barycentric coordinates](https://en.wikipedia.org/wiki/Barycentric_coordinate_system) for triangles.
If $p$ lies inside the triangle $\mathcal{T}(a,b,c)$, then there is a unique barycentric formulation:
$$p = \lambda_1 a + \lambda_2 b + \lambda_3 c$$
with $\lambda_i\geq 0$ and $\sum \lambda_i=1$.
Barycentric weights are widely used in computer graphics to linearly interpolate vertex based value to points in $T$. For instance, if you attach colors to vertices, you define a linear blending as:
$$color(p) = \lambda_1 color(a) + \lambda_2 color(b) + \lambda_3 color(c)$$
(as long as you have considered your color space as a linear vector space).
![](https://raw.githubusercontent.com/dcoeurjo/CGDI-Practicals/main/2-Rasterization/triangle.svg =300x300)
For triangles, barycentric coordinates can be easily computed from signed area as:
$$\lambda_1=\frac{Area(cpb)}{Area(abc)},\quad \lambda_2=\frac{Area(apc)}{Area(abc)},\quad \lambda_3=\frac{Area(apb)}{Area(abc)}\,.$$
Computing the $\lambda_i$ and checking whether they are all positive is a way to test if $p$ is inside $\mathcal{T}$ (this exacly corresponds to the test of the first section of this note).
10. Implement the barycentric coordinate method and interpolate colors using the barycentric linear blending.
11. Again, what can be done to design an as efficient as possible barycentric coordinate for triangle computation?
## The z-Buffer
The [z-Buffer](https://en.wikipedia.org/wiki/Z-buffering) is one of the key ingredients in many realtime rendering techniques. Let us assume a set of triangles $\{\mathcal{T}_i\}$ with an $z$ component for the vertex coordinates. Such $z$ or *depth* components correspond to the projection of the 3D points into the 2D screen. We won't go into details here but keep in mind that changes of basis (from the 3d world to the camera frame) and the projection step (orthographic or pinhole according to the camera model) can be performed using a simple matrix/vector multiplication on homogeneous coordinates (cf the lecture).
The **z-buffer** corresponds to an image buffer in which each pixel contains the depth (and the triangle id) of the closest triangle. The algorithm is pretty simple: Init a depth buffer with $+\infty$ values. For each triangle $\mathcal{T}_i$, raster $\mathcal{T}_i$ while interpolating the depth information from the vertices to inner pixels $p$, and store the depth information into an image keeping the closest triangle at that point (`zbuffer(p) = min( depth(p), zbuffer(p)` and the same for the triangle id).
At the screen resolution, the z-buffer is a very efficient solution (usually baked in the graphic pipeline of GPUs) to solve the visibility issue of 3D projected triangles.
![](https://upload.wikimedia.org/wikipedia/commons/thumb/4/4e/Z_buffer.svg/372px-Z_buffer.svg.png)
11. Implement a z-buffer using the barycentric coordinate rasterizer (random triangles with random depth values for the triangles).
12. Mix the linear color blending scheme with the z-buffer.
# Winding numbers in 2D
When dealing with more complex objects like non-simple polygonal curves (which may not be closed, with self-intersections, with multiple components..), defining and "inside" from an "outside" is a critical step in many computer graphics applications. Please refer to [^b1] and [^b2] for further details on the subject (and extensions to meshes and point cloud).
On the smooth setting, the [winding number](https://en.wikipedia.org/wiki/Winding_number) at a point $p$ is the number of times the curve wraps around $p$ in the counter-clockwise direction:
$$w(p)=\frac{1}{2\pi}\int_C d\theta\,.$$
![](https://upload.wikimedia.org/wikipedia/commons/a/ac/Winding_Number_Animation_Small.gif)
If the winding number is zero, then $p$ is outside the curve. Otherwise, it is a integer index (for closed curve) accounting for the number of nested loops $p$ belongs to:
![](https://raw.githubusercontent.com/dcoeurjo/CGDI-Practicals/main/2-Rasterization/jacobson-et-al-2013.png)[^b1]
For open polygonal curve, $w(p)$ is not an integer anymore and can be computed by summing the solid angle at $p$:
![](https://raw.githubusercontent.com/dcoeurjo/CGDI-Practicals/main/2-Rasterization/jacobson-et-al-2013-bis.png)[^b1]
$$w(p) = \frac{1}{2\pi}\sum_{i=1}^n \theta_i$$
The winding number map is now a smooth (harmonic) function that is zero, or close to zero outside, and which is positive inside.
![](https://raw.githubusercontent.com/dcoeurjo/CGDI-Practicals/main/2-Rasterization/jacobson-et-al-2013-ter.png)[^b1]
13. Express $\theta_i$ (or its tangent) from $p,c_i$ and $c_{i+1}$.
14. Given an open, non-simple polygonal object (sequence of vertices), write the function to export the Winding Number map (color map of the Winding Number at each point of a domain).
# References
[^b1]: Jacobson, A., Kavan, L., & Sorkine-Hornung, O. (2013). Robust inside-outside segmentation using generalized winding numbers. ACM Transactions on Graphics, 32(4). https://doi.org/10.1145/2461912.2461916
[^b2]: Barill, G., Dickson, N. G., Schmidt, R., Levin, D. I. W., & Jacobson, A. (2018). Fast winding numbers for soups and clouds. ACM Transactions on Graphics, 37(4). https://doi.org/10.1145/3197517.3201337

152
notes_backup/3_modeling.md
View File

@ -1,152 +0,0 @@
[CGDI] 3d modeling and geometry processing (1)
===
> [name="David Coeurjolly"]
ENS [CGDI](https://perso.liris.cnrs.fr/vincent.nivoliers/cgdi/) Version
[TOC]
---
The objective of the practical is to play with elementary 3D structures and 3d modeling of objects.
# Setting up your project with [polyscope](https://polyscope.run)
In order to focus on the geometrical algorithms (rather than technical details that may be important but slightly out-of-context here), we would like you to consider [polyscope](https://polyscope.run) for the visualization of 3d structures with attached data.
![](http://polyscope.run/media/teaser.svg)
[Polyscope](https://polyscope.run) is available in `python` or `c++` with a very similar API. The main design is that you have **structures** (point cloud, meshes, curves...) and **quantities** (scalars or vectors) attached to geometrical elements (points, vertices, edges, faces,...).
1. Update the `clone` of the repository: [https://github.com/dcoeurjo/CGDI-Practicals](https://github.com/dcoeurjo/CGDI-Practicals) (`git pull`).
* If you are using `python`: `pip install polyscope numpy`, and run the demo: `python demo.py`
* If you are using `c++`: get polyscope and its dependencies as submodules using `git submodule update --init --recursive`. Use cmake to build the project and you should get a `demo` executable.
`Python` code snippet:
``` python
import polyscope
import numpy as np
pts = np.array([[0,0,0], [0,0,1], [0,1,0], [1,0,0], [1,1,0],[0,1,1],[1,0,1],[1,1,1]])
val = np.array([ 0.3, 3.4, 0.2, 0.4, 1.2, 4.0,3.6,5.0])
polyscope.init()
polyscope.register_point_cloud("My Points", pts)
polyscope.get_point_cloud("My Points").add_scalar_quantity("Some values",val)
polyscope.show()
```
`C++` code snippet:
``` c++
#include <vector>
#include <array>
#include <polyscope/polyscope.h>
#include <polyscope/point_cloud.h>
#include <polyscope/surface_mesh.h>
int main(int argc, char **argv)
{
// Initialize polyscope
polyscope::init();
//Some data
std::vector<std::array<double, 3>> pts={{0,0,0}, {0,0,1}, {0,1,0}, {1,0,0}, {1,1,0},{0,1,1},{1,0,1},{1,1,1}};
std::vector<double> values = {0.3, 3.4, 0.2, 0.4, 1.2, 4.0,3.6,5.0};
auto pcl = polyscope::registerPointCloud("My Points", pts);
pcl->addScalarQuantity("Some values", values);
// Give control to the polyscope gui
polyscope::show();
return EXIT_SUCCESS;
}
````
2. Have a look to the [polyscope.run](https://polyscope.run) webpage, and more precisely the [structures vs. quantities](https://polyscope.run/structures/structure_management) approach.
A key ingredient of this viewer is that you can easily debug geometrical quantities attached to 3d elements with a very [generic way](https://polyscope.run/data_adaptors/) to describe those elements. For instance (in `c++`), a scalar quantity could either be a `std::vector<double>`, a `double*`, a `std::array<double>`, an `Eigen::VectorXd`... The program uses template metaprogramming and type inference to make the life of the dev easier.
The same holds for geometrical quantities, a point cloud (collection of points in $\mathbb{R}^3$) could be represented as a `std::vector< std::array<double,3> >` or as a $n\times 3$ [Eigen](https://eigen.tuxfamily.org) matrix on real numbers.
3. Create a simple program that uniformly sample the unit ball with points. Add quantities to visualize, for each sample the distance to the ball center, and the direction to its closest point. Play a bit with the various color maps and the parameters that controls the visualization.
:::info
To generate uniform numbers in $[0,1)$ you can consider `numpy.random.random()` in python or `std::uniform_real_distribution<double> distribution(0.0,1.0);` in c++.
:::
4. Generate another point set with points sampling **uniformly** the unit sphere (aka, constant density all over the domain). (*Hint*: have a look to the first practical)
# Modeling 101
As described in the lecture, the simplest way to describe a polygonal surface is to consider an structure for the vertex coordinates (*e.g.* $|V|\times 3$ `numpy` array or `std::vector<std::array<double,3>>`):
```
v1: x1 y1 z1
v2: x2 y2 z2
v3: x3 y3 z3
...
```
and an array for faces (*e.g* vector of vectors) where each face is described by a sequence of vertex indices:
```
f1: id1 id2 id3 id4
f2: id3 id4 id5
...
```
(in this example, the first face has four vertices and share an edge with the second triangular one). So
5. Create a new [Surface Mesh](https://polyscope.run/structures/surface_mesh/basics/) structure in polyscope representing a unit cube.
6. For each face, compute the normal vector (unitary vector perpendicular to the face) and visualize it as a [vector quantity](https://polyscope.run/structures/surface_mesh/vector_quantities/).
7. For each face again, do the math and create a per face orthogonal frame (two additional vectors to encode the tangent plane at the face): ![](https://raw.githubusercontent.com/dcoeurjo/CGDI-Practicals/main/3-modeling/Capture%20d’écran%202021-02-02%20à%2012.43.32.png =200x)
8. Attach a quantity to each vertex that corresponds to the abscissa of that vertex.
::: info
Internally, the 3d viewer uses the same linear blending scheme on the faces as the one you have implemented in the previous practical.
:::
9. Generate an object made of randomly shifted, scaled and rotated cubes (cf the lecture for the transformation matrices).
# Catmull-Clark Subdivision Scheme
The idea now is to implement a basic yet widely used [subdivision surface](https://en.wikipedia.org/wiki/Subdivision_surface) scheme: the [Catmull-Clark](https://en.wikipedia.org/wiki/Catmull–Clark_subdivision_surface) scheme.
:::success
Ed Catmull = co-funder of Pixar ;). Nice [paper](https://graphics.pixar.com/library/Geri/paper.pdf) about subdivision surfaces in character animation from Pixar.
:::
![](https://upload.wikimedia.org/wikipedia/commons/3/33/Catmull-Clark_subdivision_of_a_cube.svg =200x)
Starting from a quadrilateral mesh, the limit surface is a bicubic [B-spline](https://en.wikipedia.org/wiki/B-spline) surface. The implicit limit surface is widely used in rendering with for instance very efficient ray/surface intersections without explicitly computing the high-resolution surface.
10. Starting from a unit cube, create a single [Catmull-Clark step](https://en.wikipedia.org/wiki/Catmull–Clark_subdivision_surface). To do so, you would need to implement several traversal/topological functions: iterate through the vertices of a face, to retrieve the two faces associated with an edge...
::: info
For the data structure and polyscope side, just keep it simple at this point: to subdivide a mesh, just create a new face-vertex structure (and `register` it in polyscope) and delete the previous one (instead of doing smart updates in the structures).
:::
11. Perform several subdivision steps to converge to a smooth object (be careful about the combinatorics...).
12. Have a look to the various [alternative schemes](https://en.wikipedia.org/w/index.php?title=Subdivision_surface&section=3) that have been proposed for the triangular or quadrangular cases.
# Additional Stuff: loading OBJ 3d model
We just detail here few hints in `python` or `c++` to visualize [Wavefront OBJ file](https://en.wikipedia.org/wiki/Wavefront_.obj_file) (simple ascii file easy to parse).
In `python`, you can have a look to [pygel3d](http://www2.compute.dtu.dk/projects/GEL/PyGEL/) (package that Vincent is using for the lecture, `pip install pygel3D`). The package comes with an visualization toolkit but have a look to the `testpyGEL.py` for an OBJ loading example with visualization using polyscope. The package also contains a manifold mesh API (to iterate of the mesh elements for instance) that we may be using for the next practicals.
In `c++`, there are various alternatives ([CGAL](http://cgal.org), [libIGL](https://libigl.github.io), [openmesh](https://www.openmesh.org)...). At this point, I will showcase the [geometry-central](https://geometry-central.net) lib that fits well with polyscope. Have a look to the practicals repository for a demo (geomtry-central has been added as `git submodule`, just do the update as mentioned at the very beginning of the note). Just have a look to the `displayOBJ.cpp` file.
![](https://raw.githubusercontent.com/dcoeurjo/CGDI-Practicals/main/3-modeling/bimba.png)